알고리즘 - Dynamic Programming(동적 계획법)
Dynamic Programming 이란?
최적화이론의 한 기술이며, 특정 범위까지의 값을 구하기 위해서 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는알고리즘 설계 기법이다.
Dynamic Programming Algorithm의 해결 방법은
입력 크기가 작은 부분 문제들을 모두 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분문제들을 해결하여 최종적으로 원래 주어진 입력의 문제를 해결한다.
덧붙여서 설명하자면 복잡한 문제를 간단한 여러개의 문제로 나누어 푼다는 것이다.
동적 알고리즘의 개념으로 모든 쌍 최단 경로, 연속 행렬 곱셈, 편집 거리 문제, 배낭 문제들을 공부해볼 예정이다
구현
Dynamic Programming의 접근방식은 분할 정복 알고리즘과 비슷하다. Dynamic Programming을 사용하는 알고리즘 역시 주어진 문제를 간단한 여러개의 문제로 나누어 푼다.
분할 정복과의 차이점은 문제를 나누는 방식에서 차이가 생긴다. Dynamic Programming의 경우에는 문제를 여러개의 문제로 나눈 다음, 부문 문제의 정답을 한 번만 계산하고 저장한다. 그리하여 다시 부문 문제를 풀어야할 때 저장해둔 정답을 가져와 이용함으로 속도를 향샹시킨다.
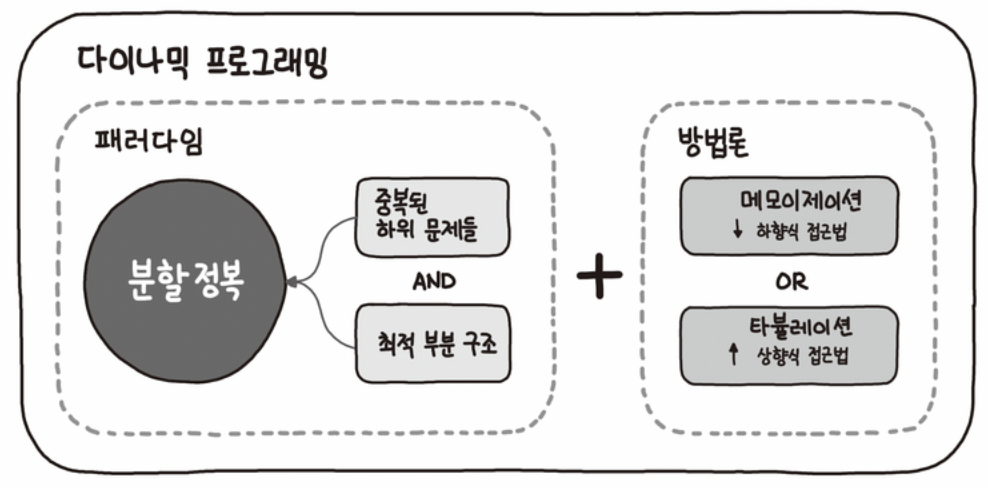
즉, Dynamic Programming은 중복된 하위 문제들에 대해 반복 계산하지 않고 단 한번만 풀도록 하는 알고리즘이다.
예시
Dynamic Programming을 이해하는 가장 쉬운 예시는 피보나치 수열이라고 생각한다. 피보나치 수열은 다음과 같이 재귀함수의 형태(Recursive Form)으로 표현된다.
- F[0] = 0
- F[1] = 1
- F[N] = F[N-1] + F[N-2] (N ≥ 2)
피보나치 수열을 분할 정복 알고리즘을 사용하여 해결한다면 함수의 재귀적 호출로 인한 메모리가 많이 쓰여지는 현상이 발생한다. 숫자가 조금만 커져도 시간 복잡도와 공간 복잡도가 지수 스케일로 증가한다….
Dynamic Programming에서는 이런 문제들을 막기위해 한번 계산했던 값들을 배열에 저장한다. 대표적인 방식으로는 Top-down과 Bottom-up이 있는데 Top-down방식은 큰문제를 작은 문제로 나누어서 해결한다는 것이고 Bottom-up는 작은 문제에서 시작하여 문제를 점점 쌓아 큰 문제를 해결한다는 것이다.
예를들어 Top-down은 F[4]을 구하는 문제는 F[3]와 F[2]로 F[3]은 다시 F[2]와 F[1]로 나누는 방식이고 Bottom-up은 F[3] = F[2] + F[1]로 해결하는 방식으로 이해하면 된다.
A Java Example(Top-down):
int fibonacci(int n){
if(n == 0)
return 0;
if(n == 1)
return 1;
if(DP[n] != 0){
return DP[n];
}
DP[n] = fibonacci(n - 1) + fibonacci(n - 2);
return DP[n];
}
A Java Example(Bottom-up):
int fibonacci(int n){
DP[0] = 0;
DP[1] = 1;
for(int i = 2; i <=n; i++){
DP[i] = DP[i - 1] + DP[i - 2];
}
}
즉, Dynamic Programming에서 한번 계산했던 값들을 배열에 저장하는데 이것을 DP(Dynamic Programming)‘메모이제이션(Memoization)’이라고 한다. 이미 계산한 결과는 배열에 저장함으로써 동일한 계산을 해야할 때는 저장된 배열의 값을 반환하기만 하면 된다.
Memoization을 사용하지 않고 재귀를 이용하여 구하면 수가 커질수록 함수호출이 많아지기 때문에 오래 걸린다. (시간 복잡도 : O(2N))
A Java Example(Recursive Call):
int fibonacci(int n){
if(n <= 1){
return n;
}
else{
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
하지만 Memoization을 사용한다면 한번 계산한 부분은 다시 계산하지 않기때문에 훨씬 빠르게 작동한다. (시간 복잡도 : O(f(N)))
static int[] DP = new int[N]; //배열의 크기는 정의하기 나름이다.
static int memoizationFibo(int n){
if(n == 0)
return DP[0];
if(n == 1)
return DP[1];
if(DP[n] != 0)
return DP[n];
return DP[n] = memoizationFibo[n - 1] + memoizationFibo[n - 2];
}
오늘은 Dynamic Programming에 대해 정리해 보았으니 뒤에는 관련된 문제를 풀거나 추가적인 알고리즘을 정리해 포스팅 해보도록 해야겠다.