Dijkstra Algorithm 이란?

Dijkstra Algorithm(다익스트라 알고리즘)은 그래프의 출발점으로 부터 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다.

Dijkstra Algorithm은 한 정점에서 다른 정점까지의 최단 경로를 찾는데 사용되며, 가중치가 있는 유향 그래프에서 주로 사용된다. 조건은 weighted graph이어야 하고 starting point가 있어야 한다.

임의의 점을 하나 선택한 후, (n - 1)개의 선분을 하나씩 추가하여 트리를 만든다

Dijkstra Algorith은 그리디(greedy) 알고리즘의 일종으로, 현재 정점에서 가장 거리값이 작은 정점을 선택하여 최단 경로를 찾는 방식으로 동작한다. 정점의 개수를 V, 간선의 개수를 E 라고 하면 O(ElogV)의 시간 복잡도를 가진다.

Dijkstra Algorithm 과정

1. 출발점에서의 거리 값을 초기화 한다. 출발점은 0으로, 다른 정점은 무한대로 설정한다.
2. 방문하지 않은 정점들 중에서 거리 값이 가장 작은 정점을 선택한다.
3. 현재 정점과 인접한 정점들의 거리 값을 갱신한다. 현재 정점을 통해 인접한 정점으로 가는 거리가 짧다면 해당 인접 정점의 거리 값을 갱신한다.
4. 현재 정점을 방문한 것으로 표시한다.
5. 출발점으로부터 모든 정점들 까지의 거리 값을 갱신할 때 까지 2 ~ 4를 반복한다.
6. 모든 정점들의 거리 값이 갱신되면 최단 경로가 구해진다.


Dijkstra Pseudo-code(ShortestPath)

입력 : 가중치 그래프 G = (V, E) , |V| = n(점의 수), |E| = m(간선의 수)

출력 : 출발점 s로 부터 (n - 1)개의 점까지 각각 최단 거리를 저장한 배열 D

1. 배열 D를 무한대로 초기화. D[s] = 0으로 초기화.
    //배열 D[v]에는 출발점 s로부터 점 v 까지의 거리가 저장.

2. while(s로부터의 최단 거리가 확정되지 않은 점이 있으면){

3.  현재까지 s로부터 최단 거리가 확정되지 않은 각 점 v에 대해서 최소 D[v]의 값을 가진
    점 vmin을 선택하고, 출발점 s로부터 점 vmin까지의 최단거리 D[vmin]을 확정

4.  s로부터 현재보다 짧은 거리로 점 vmin을 통해 우회 가능한 각 점 w에 대해서 D[w]를 갱신 }

5. return D




{
    T ← Ф ; ▷ T : 정점 집합
    for each u∈V
        d[u] ← ∞ ;
        d[s] ← 0 ;
    while (T≠V ) { ▷ n회 순환된다
        u ← extractMin(V-T, d) ;
        T ← T ∪{u};
        for each v∈L(u) ▷ L(u) : u로부터 연결된 정점들의 집합
        if (v∈V-T and d[u] +w[u, v] < d[v] ) then {
            d[v] ← d[u] + w[u, v];
            prev[v] ← u;
        }
    }
}
    extractMin(Q, d[])
{
    집합 Q에서 d값이 가장 작은 정점 u를 리턴한다 ;
}

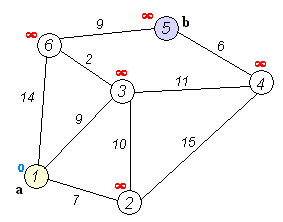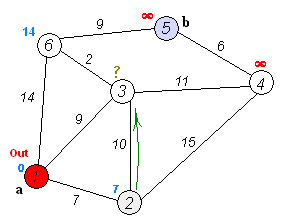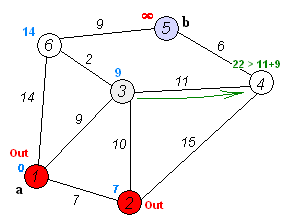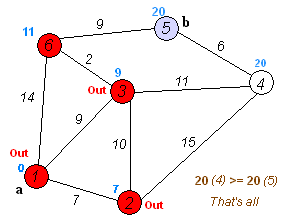Dijkstra 출처:https://upload.wikimedia.org/wikipedia/commons/5/57/Dijkstra_Animation.gif

Dijkstra Algorithm 구현

import java.util.*;

public class DijkstraAlgorithm {
    public static int[] dijkstra(int[][] graph, int start) {
        int n = graph.length; // 그래프의 크기
        int[] distances = new int[n]; // 최단 거리를 저장할 배열
        boolean[] visited = new boolean[n]; // 방문 여부를 저장할 배열

        Arrays.fill(distances, Integer.MAX_VALUE); // 초기 거리를 무한대로 설정
        distances[start] = 0; // 시작점의 거리를 0으로 설정

        for (int i = 0; i < n; i++) {
            int minDist = Integer.MAX_VALUE;
            int minVertex = -1;

            // 아직 방문하지 않은 정점 중에서 최소 거리를 가진 정점을 선택
            for (int j = 0; j < n; j++) {
                if (!visited[j] && distances[j] < minDist) {
                    minDist = distances[j];
                    minVertex = j;
                }
            }

            if (minVertex == -1) {
                break; // 모든 정점을 방문한 경우 종료
            }

            visited[minVertex] = true; // 최소 거리를 가진 정점 방문 처리

            // 선택한 정점을 통해 갈 수 있는 다른 정점들의 거리를 갱신
            for (int j = 0; j < n; j++) {
                if (!visited[j] && graph[minVertex][j] != 0 && distances[minVertex] != Integer.MAX_VALUE
                        && distances[minVertex] + graph[minVertex][j] < distances[j]) {
                    distances[j] = distances[minVertex] + graph[minVertex][j];
                }
            }
        }

        return distances;
    }

    public static void main(String[] args) {
        int[][] graph = {   { 0, 2, 5, 0, 0, 0 },
                            { 2, 0, 4, 6, 10, 0 },
                            { 5, 4, 0, 2, 0, 0 },
                            { 0, 6, 2, 0, 0, 1 },
                            { 0, 10, 0, 0, 0, 3 },
                            { 0, 0, 0, 1, 3, 0 } }; // 가중치 그래프
        int start = 0; // 출발점

        int[] distances = dijkstra(graph, start);

        System.out.println("출발점 " + start + "로부터의 최단 거리:");
        for (int i = 0; i < distances.length; i++) {
            System.out.println("정점 " + i + ": " + distances[i]);
        }
    }
}

실행 결과

출발점 0로부터의 최단 거리:
정점 0: 0
정점 1: 2
정점 2: 5
정점 3: 7
정점 4: 11
정점 5: 8