알고리즘 - Prim Algorithm(프림 알고리즘)

Prim Algorithm 이란?

Prim Algorithm(프림 알고리즘)은 최소 신장 트리(Minimum Spanning Tree)를 찾는 알고리즘이다. 시작 정점에서 출발하여 해당 정점과 연결된 간선 중에서 가중치가 가장 적은 간선을 선택하여 해상 간선으로 연결된 정점을 트리에 추가하는 과정을 반복한다.

임의의 점을 하나 선택한 후, (n - 1)개의 선분을 하나씩 추가하여 트리를 만든다

Prim Algorith의 시간 복잡도는 간선의 개수를 E, 정점의 개수를 V 라고 할 때, 우선순위 큐를 배열로 구현할 경우, 모든 정점에 대해서 우선순위 큐에 새로운 원소를 삽입하고 최솟값을 찾는 과정을 V번 반복하기 때문에 O(V^2)의 시간 복잡도를 가집니다.

하지만 우선순위 큐를 힙(heap)으로 구현할 경우, 각 정점마다 우선순위 큐에 새로운 원소를 삽입하는 것이 아니라, 이미 삽입된 원소 중에서 최솟값을 찾아서 삭제하는 과정을 E번 반복하게 됩니다. 따라서 시간 복잡도는 O(E log V)가 됩니다.

Prim Algorithm 과정

1. 시작 정점을 선택하고, 해당 정점과 연결된 모든 간선을 우선순위 큐에 삽입한다.
2. 우선순위 큐에서 가장 가중치가 작은 간선을 선택하고, 해당 간선으로 연결된 정점을 트리에 추가한다.
3. 새로 추가된 정점과 연결된 간선 중에서, 트리와 연결된 간선은 우선순위 큐에서 제거하고, 트리와 연결되지 않은 간선은 우선순위 큐에 삽입한다.
4. 우선순위 큐가 비어 있을때 까지 2 ~ 3번을 반복한다.

Prim Pseudo-code

입력 : 가중치 그래프 G = (V, E) , |V| = n(점의 수), |E| = m(간선의 수)

출력 : 최소 신장 트리 T

그래프 G에서 임의의 점 p를 시작점으로 선택하고 D[p]=0으로 놓는다.

for (점 p가 아닌 각 점 v에 대하여) { // D 초기화 과정

if ( 선분 (p,v)가 그래프에 있으면)

D[v] = 선분 (p,v)의 가중치

else

D[v]=∞ }

T= {p}

while (T에 있는 점의 수 < n) { // T 업데이트

T에 속하지 않은 각 점 v에 대하여, D[v]가 최소인 점 vmin과 연결된 선분 (u,vmin)을 T에 추가한다. 단, u는

T에 속한 점이고, 점 vmin도 T에 추가된다.

for (T에 속하지 않은 각 점 w에 대해서) { // D 업데이트

if (선분 (vmin,w)의 가중치 < D[w])

D[w] = 선분 (vmin,w)의 가중치} }

return

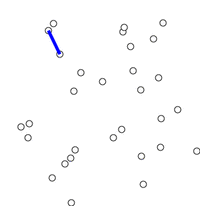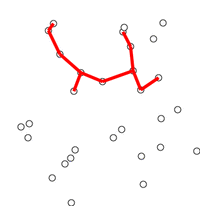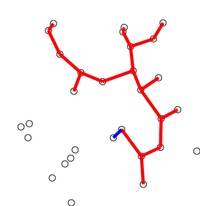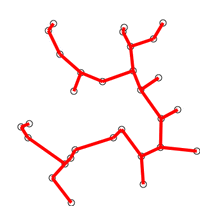Kruskal 출처:https://upload.wikimedia.org/wikipedia/commons/thumb/9/9b/PrimAlgDemo.gif/200px-PrimAlgDemo.gif

Prim Algorithm 구현

import java.util.*;

public class App {
    private static final int INF = 9999999;

    private int[][] graph; // 인접 행렬로 그래프 표현
    private int[] D; // 시작점으로부터의 거리 저장
    private boolean[] visited; // 해당 노드를 방문했는지 여부 저장
    private int n; // 노드의 개수

    public App(int[][] graph) {
        this.graph = graph;
        n = graph.length;
        D = new int[n];
        visited = new boolean[n];
    }

    private int minDistance() {
        int min = INF, min_index = -1;
        for (int i = 0; i < n; i++) {
            if (!visited[i] && D[i] < min) {
                min = D[i];
                min_index = i;
            }
        }
        return min_index;
    }

    public int[][] findMinimumSpanningTree(int start) {
        // D 초기화
        for (int i = 0; i < n; i++) {
            if (graph[start][i] != 0) {
                D[i] = graph[start][i];
            } else {
                D[i] = INF;
            }
            visited[i] = false;
        }
        visited[start] = true;
        int count = 1;

        int[][] T = new int[n - 1][2]; // 최소 신장 트리 저장 배열
        int t = 0; // T의 인덱스

        while (count < n) {
            int vmin = minDistance();
            visited[vmin] = true;
            for (int w = 0; w < n; w++) {
                if (graph[vmin][w] != 0 && !visited[w] && graph[vmin][w] < D[w]) {
                    D[w] = graph[vmin][w];
                }
            }
            T[t][0] = vmin;
            T[t][1] = findParent(vmin);
            t++;
            count++;
        }
        return T;
    }

    private int findParent(int child) {
        for (int i = 0; i < n; i++) {
            if (graph[child][i] == D[child] && visited[i]) {
                return i;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int m = sc.nextInt();

        int[][] graph = new int[n][n];
        for (int i = 0; i < m; i++) {
            int u = sc.nextInt();
            int v = sc.nextInt();
            int w = sc.nextInt();
            graph[u][v] = w;
            graph[v][u] = w;
        }

        App prim = new App(graph);
        int[][] T = prim.findMinimumSpanningTree(0);

        System.out.println("Edges of the minimum spanning tree:");
        for (int[] edge : T) {
            System.out.println(edge[0] + " - " + edge[1]);
        }
    }
}

예제 입력

실행 결과

Edges of the minimum spanning tree:
- 0
- 0
- 2
- 3