자료구조 - Priority Queue(우선순위 큐)

Priority Queue 란?

보통의 큐는 형식의 먼저 들어온 데이터가 먼저 나가게 되는 선입 선출(FIFO : First-in First-out)의 형식이다. 우선순위 큐(Priority Queue)는 데이터 들의우선순위를 가져 우선순위가 높은 데이터가 먼저 나가게된다.

우선순위 큐(Priority Queue)는 배열, 연결 리스트 등의 여러 가지 방법으로 구현이 가능한데, 가장 효율적인 구조는힙(Heap)이다. 힙(Heap)을 사용해서 우선순위 큐를 구현해보자.

---

Heap 이란?

힙(Heap)은 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조이다.

힙(Heap)은 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진 트리을 말한다.

Key(부모노드) ≥ Key(자식노드)

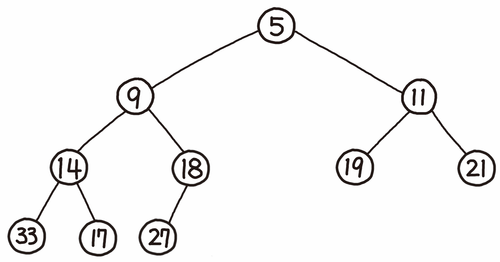
위 사진은 최소 힙(min heap)이다

힙 트리(Heap Tree)에서는 중복된 값을 허용하며 완전 이진 트리(Complete binary tree)이다.

---

Heap 종류

• 최대 힙(max heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리.

  Key(부모노드) ≥ Key(자식노드)

• 최소 힙(min heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리.

  Key(부모노드) ≤ Key(자식노드)

---

Heap의 정의

힙(Heap)은 1차원 배열로 표현될 수 있다.

#define MAX_ELEMENT 100
typedef struct{
    int key;
}element;
typedef struct{
    element heap[MAX_ELEMENT];
    int heap_size;
}HeapType;

Heap의 구현

---

• insert() : 마지막 위치에 새로은 요소 X를 삽입후 부모노드와 계속 비교하여 부모노드보다 작을 때까지 교환한다.

void insert_max_heap(HeapType* h, element item){
    int i;
    i = ++(h->heap_size);

    //Tree를 올라가면서 부모 노드와 비교
    while((i != 1) && (item.key > h->heap[i / 2].key)){
        h->heap[i] = h->heap[i / 2];
        i /= 2;
    }
    //새로운 노드 삽입
    h->heap[i] = item;
}

• delete() : 루트 노드를 삭제후 마지막 노드를 가져온 다음, 자식노드와 계속 비교하여 자식노드보다 클 때 까지 교환한다.

element delete_max_heap(HeapType* h){
    int parent, child;
    element item, temp;

    item = h->heap[1];
    temp = h->heap[(h->heap_size)--];
    parent = 1;
    child = 2;

    while(child <= h->heap_size){
        //자식 노드중 더 큰 자식 노드를 찾는다
        if((child < h->heap_size) && (h->heap[child].key) < h->heap[child + 1].key)
            child++;
        if(temp.key >= h->heap[child].key)
            break;
        //한 단계 아래로 이동
        h->heap[parent] = h->heap[child];
        parent = child;
        child *= 2;
    }
    h->heap[parent] = temp;
    return item;
}