알고리즘 - Floyd-Warshall Algorithm(플로이드-워샬 알고리즘)

Floyd-Warshall Algorithm 이란?

Floyd-Warshall Algorithm(플로이드-워샬 알고리즘)은 모든 점에 대해서 다른 모든 점에대한 경로를 찾을수 있고 음의 가중치를 가진 그래프에서도 사용할 수 있다.

Warshall은 그래프에서 모든 쌍의 경로 존재 여부를 찾아내는 동적 계획 알고리즘을 제안했다.

Floyd는 이를 변형하여 모든 쌍 최단 경로를 찾는 알고리즘을 고안하여 모든 쌍 최단 경로를 찾는 동적 계획 알고리즘을 플로이드-워샬 알고리즘이라고 한다.

플로이드 알고리즘의 시간 복잡도는 O(n^3)으로 다익스트라 알고리즘을 n번 사용할 때의 시간 복잡도와 동일하다. 플로이드 알고리즘을 매우 간단하며 다익스트라 알고리즘을 사용하는 것 보다 효율 적이다.

Floyd-Warshall Algorithm 과정

Floyd-Warshall Algorithm Pseudo-code

입력: 2차원 배열 D, 단 D[i,j]=간선(i,j)의 가중치, 만일 간선 (i,j)이 존재하지 않는다면, D[i,j]= inf, 모든 i에 대하여 D[i,j]=0이다.
출력: 모든 쌍의 최단 경로의 거리를 저장한 2차원 배열 D
1. for k = 1 to n
2. 	for i=1 to n (단 i!=k)
3. 		for j=1 to n (단, j!=k,j!=i)
4. 			D[i,j] = min{D[i,k]+D[k,j],D[i,j]}

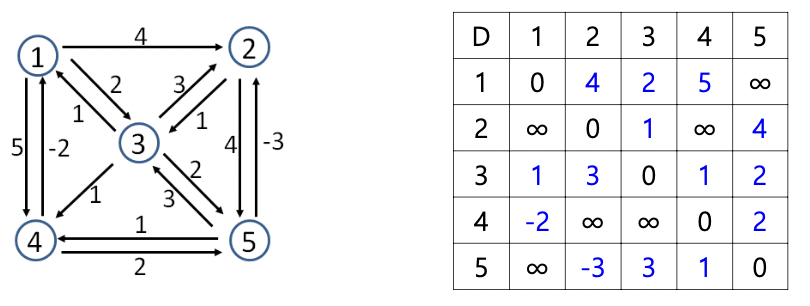
FloydWarshall

Floyd-Warshall 알고리즘은 그래프에서 transitive closure을 찾는것이다.

transitive closure는 그래프 이론에서 사용되는 개념으로, 유향 그래프에서 한 정점에서 다른 모든 정점으로 가는 경로가 존재하는 경우, 두 정점은 ‘도달 가능’(reachable)하다고 말합니다. 이때, 해당 그래프에서 모든 정점 쌍 간의 도달 가능 여부를 표시한 행렬을 transitive closure 행렬이라 한다.

transitive closure 구하기: dist 배열의 값이 무한대가 아닌 경우, 해당 노드 쌍은 도달 가능합니다. 따라서, dist 배열의 값이 무한대인 노드 쌍은 도달 불가능하다고 판단할 수 있습니다. 이를 이용하여, transitive closure 행렬을 구할 수 있다.

부분 문제들을 찾은후 모든 점을 경유 가능한 점들로 고려하면서 모든 쌍의 최단 경로의 거리를 계산한다

Floyd-Warshall Algorithmm 구현

public class FloydWarshallAlgorithm {
    public static int[][] floydWarshall(int[][] D) {
        int n = D.length;

        // 거리 배열 초기화
        int[][] dist = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                dist[i][j] = D[i][j];
            }
        }

        // 플로이드-와샬 알고리즘 수행
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (dist[i][k] != Integer.MAX_VALUE &&
                            dist[k][j] != Integer.MAX_VALUE &&
                            dist[i][k] + dist[k][j] < dist[i][j]) {
                        dist[i][j] = dist[i][k] + dist[k][j];
                    }
                }
            }
        }

        return dist;
    }

    public static void main(String[] args) {
        int INF = Integer.MAX_VALUE;

        int[][] D = {
                {0, INF, 3, INF},
                {2, 0, INF, INF},
                {INF, 7, 0, 1},
                {6, INF, INF, 0}
        };

        int[][] dist = floydWarshall(D);

        // 최단 경로 출력
        for (int i = 0; i < dist.length; i++) {
            for (int j = 0; j < dist.length; j++) {
                if (dist[i][j] == INF) {
                    System.out.print("INF ");
                } else {
                    System.out.print(dist[i][j] + " ");
                }
            }
            System.out.println();
        }
    }
}

실행 결과