자료구조 - Tree(트리)

Tree란?

트리(Tree)는 계층적인 자료를 표현하는데 적합한 자료구조이며, 그래프의 일종으로 한 노드에서 시작해서 다른 노드를 순회하여 자기 자신으로 돌아오는 순환이 없는 연결 그래프이다.

즉 트리(Tree)는 한 개 이상의노드(node)이루어진 자료구조 이다.

Tree의 용어

루트 노드(root node) : 계층적인 구조에서 가장 높은 곳에 있는 노드. 부모가 없는 노드. 트리는 하나의 노드를 가진다.
자식 노드(leaf node) : 자식이 없는 노드, ‘잎 노드’ ‘말단 노드’ 라고 부른다.
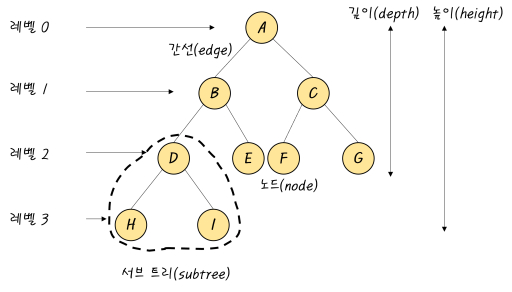
간선(edge) : 노드와 노드간을 연결 하는 선.
차수(degree) : 어떤 노드가 가지고 있는 자식 노드의 개수.
레벨(level) : 트리의 각 층에 번호를 매기는 것.
높이(height) : 트리가 가지고 있는 최대 레벨을 말한다.
깊이(depth) : 루트 경로의 길이를 뜻한다.
크기(size) : 노드의 개수.

DataStructure_Tree

Tree의 종류

이진 트리(binary tree)

이진 트리(binary tree)는 모든 노드가 2개의 서브 트리를 가지고 있는 트리를 말한다. 최대 2개 까지의 자식 노드가 존재할 수 있고 모든 노드의 차수가 2 이하가 되어야 한다.

이진 트리의 분류

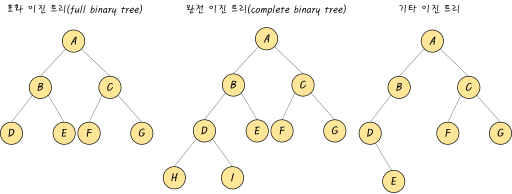
포화 이진 트리(full binary tree) : 트리의 각 레벨에 노드가 꽉 차있는 이진트리를 뜻한다. 높이 K인 포화 이진 트리는 2^k-1개의 노드를 가진다.
완전 이진 트리(complete binary tree) : 높이가 k일때 레벨 1 부터 k - 1 까지는 노드가 모두 채워져 있고 마지막 레벨 k 에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리 이다. 마지막 레벨에서는 노드가 꽉차있지 않아도 되지만 중간에 빈곳이 있어서는 안된다.
기타 이진 트리 : 노드의 개수.

DataStructure_Tree2

이진 트리의 표현

배열 표현법 : 이진트리의 깊이가 k이면 최대 2^k-1개의 공간을 연속적으로 할당한 후, 완전 이진 트리의 번호대로 노드들을 저장한다.
```
  노드 i의 부모 노드 인덱스 = i/2
  노드 i의 왼쪽 자식 노드 인덱스 = 2i
  노드 i의 오른쪽 자식 노드 인덱스 = 2i + 1
```
링크 표현법 : 트리에서의 노드가 구조체로 표현되고, 각 노드가 포인터를 가지고 있어 포인터로 노드와 노드를 연결 하는 방법이다.

typedef struct TreeNode{
    int data;
    struct TreeNode *left, *right;
} TreeNode;

이진 트리의 순회

이진트리를 순회하는 방법에는 전위, 중위, 후위 3가지 방법이 있는데, 이 차이는 루트, 왼쪽 서브트리, 오른쪽 서브트리 중에서 어느곳을 언제 방문하느냐에 따라 구분된다.

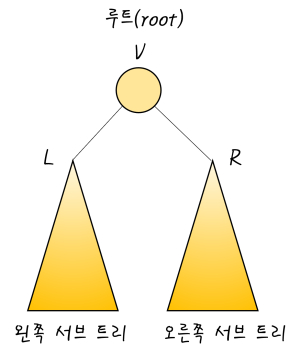
DataStructure_Tree2

전위 순회(preorder traversal) : VLR

void preorder(TreeNode *root){
    if(root != null){
        printf("[%d]", root->data);
        preorder(root->left);
        preorder(root->right);
    }
}

중위 순회(inorder traversal) : LVR

void inorder(TreeNode *root){
    if(root != null){
        inorder(root->left);
        printf("[%d]", root->data);
        inorder(root->right);
    }
}

후위 순회(postorder traversal) : LRV

void postorder(TreeNode *root){
    if(root != null){
        postorder(root->left);
        postorder(root->right);
        printf("[%d]", root->data);
    }
}

이진 탐색 트리(binary search tree)

이진 트리 기반의 탐색을 위한 자료구조이다. 이진 탐색 트리(binary search tree)는 다음의 성질을 만족하는 이진트리를 말한다.

• 모든 원소의 키는 유일한 키를 가진다
• 왼쪽 서브 트리 키들은 루트 키 보다 작다
• 오른쪽 서브 트리 키들은 루트의 키보다 크다
• 왼쪽과 오른쪽 서브트리도 이진 탐색 트리다.

이러한 성질을 이용하여 탐색을 쉽게 할 수 있다.

이진 탐색 트리 연산

탐색 연산

TreeNode* search(TreeNode *node, int key){
    while(node != NULL){
        if(key == node->key)
            return node;
        else if(key < node->key)
            node = node->left;
        else
            node = node->right;
    }
    return NULL; //탐색 실패
}

삽입 연산

트리에 원소를 삽입하기 위해서는 먼저 탐색을 해야한다. 왜냐하면 이진 탐색 트리에서는 같은 키 값을 갖는 노드가 없어야 하며, 탐색에 실패한 지점이 바로 새로운 노드를 삽입하는 위치가 되기 때문이다.

TreeNode* insert_node(TreeNode *node, int key){
    if(node == NULL)
        return new_node(key); //공백이면 새로운 노드를 반환한다.
    if(key < node->key)
        node->left = insert_node(node->left, key);
    else if(key > node->key)
        node->right = insert_node(node->right, key);

    return node;
}

삭제 연산

삭제 또한 먼저 노드를 탐색해야 한다. 하지만 삭제 연산에경우 3가지의 경우를 고려해야만 한다.

삭제하려는 노드가 단말 노드인 경우
삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리중 하나만 가지고 있는 경우
삭제하려는 노드가 두개의 서브 트리를 모두 가지고 있는 경우.

TreeNode* delete_node(TreeNode *root, int key){
    if(root == NULL)
        return root;
    if(key < root->key)
        root->left = delete_node(root->left, key); //키가 루트보다 작으면 왼쪽 서브트리
    else if(key > root->key)
        root->right = delete_node(root->right, key); //키가 루트보다 크면 오른쪽 서브트리
    //키가 루트와 같으면 이 노드를 삭제한다.
    else{
        //1. 또는 2.의 경우
        if(root->left == NULL){
            TreeNode *temp = root->right;
            free(root);
            return temp;
        }
        else if(root->right == NULL){
            TreeNode *temp = root->left;
            free(root);
            return temp;
        }
        //3. 경우
        TreeNode *temp = min_value_node(root->right);
        root->key = temp->key;
        root->right = delete_node(root->right, temp->key);
    }
    return root;
}

TreeNode* min_value_node(TreeNode *node){
    TreeNode *current = node;
    while(current->left != NULL)
        current = current->left;
    return current;
}