알고리즘 - Chained Matrix Multiplications(연속 행렬 곱셈)
Chained Matrix Multiplications 이란?
Chained Matrix Multiplications(연속 행렬 곱셈)동적 계획법(Dynamic programming)을 사용하여 연속된 행렬들의 곱셉에 필요한 원소 간의 최소 곱셉 횟수를 찾는 문제.
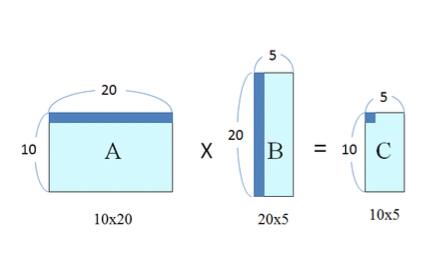
N x M 행렬 A와 r x s 행렬 B가 있고 M = r 일때 N x s 행렬 C가 가능하다
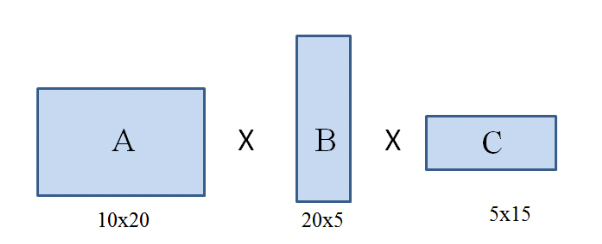
3개의 행렬을 곱해야 하는 경우에는, 연속 행렬 곱셈에는 결합 법칙이 허용되기 때문에 AxBxC = (AxB)xC = Ax(BxC)가 가능하다.
하지만 같은결과를 보여주지만 연산하는 양에따른 차이가난다. 그리하여 연산하는 양이 최소가 되는 방법을 찾아서 적용해야하는데 이때 동적 계획법 방법을 사용한다.
AxBxCxDxE = (AxB)x(CxDxE) = Ax(Bx(CxDxE))
위의 예제를 보면 ABCDE를 곱하는 것에 대한 부분문제들 중 하나인데 부분문제들이 겹쳐있는 것을 확인 할 수 있다 즉, 부분문제에 대한 연산이 중복적으로 나타나는 것을 볼 수 있다.

Chained Matrix Multiplications 과정
Matrix index start from 1 M1 x M2 M1 x M2 x M3 M1 x M2 x … x Mj ▪ f(i,j) ] min ((f(i, i+1,j), f(i, i+2,j),f(i, i+3,j), …, f(i, j-1,j))) ▪ min((f(1,2,j), f(1,3,4), f(1,4,j), …, f(1,j-1,j)) ▪ f:(x,y,z) -> N => x is the staring point, y is the splitting point, z is the final point ▪ Point : a matrix index
Algorithm Design
c[i][j] = Ai ~ Aj 곱하기 위한 최소 곱셈 수 (i < j 인 경우)
c[i][i] = 0 //diagonal init, k = split point
c[i][j] = min(c[i][k] + c[k+1][j] + di-1dkdj), i < j,(min -> i <= k <= j-1)
c[i][i] = 0, for 1 <= i <= n
Chained Matrix Multiplications Pseudo-code
입력: 연속된 행렬 A1xA2x⋯xAn, 단, A1은 d0xd1, A2는 d1xd2, ⋯, An은 dn-1xdn이다. 출력: 입력의 행렬 곱셈에 필요한 원소의 최소 곱셈 횟수
- for i = 1 to n
- C[i,i] = 0 //initialization
- for L = 1 to n - 1 { //diagonal loop
- for i = 1 to n - L {
- j = i + L
- C[i,j] = INF
- for k = i to j - 1 {
- temp = C[i,k] + C[k + 1, j] = di-1dkdj
- if(temp < C[i,j])
- C[i,j] = temp } } }
- return C[1,n]
Chained Matrix Multiplications 구현
public class ChainedMatrixMultiplication {
public static int matrixMultiplication(int[] p) {
int n = p.length - 1;
int[][] dp = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
dp[i][i] = 0;
}
for (int l = 2; l <= n; l++) {
for (int i = 1; i <= n - l + 1; i++) {
int j = i + l - 1;
dp[i][j] = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
int temp = dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j];
if (temp < dp[i][j]) {
dp[i][j] = temp;
}
}
}
}
return dp[1][n];
}
public static void main(String[] args) {
int[] p = {10, 30, 5, 60};
int result = matrixMultiplication(p);
System.out.println(result); // 4500
}
}
위 코드에서 p는 입력 행렬의 차원을 나타내는 배열입니다. p의 길이가 n+1이면, i번째 행렬의 차원은 p[i-1] x p[i]가 됩니다. 예를 들어, p = {10, 30, 5, 60}이면, 입력 행렬은 10x30, 30x5, 5x60 세 개의 행렬이 순서대로 연속되어 있는 것입니다.
위 코드에서는 dp[i][j]를 입력 행렬 A_i * A_{i+1} * … * A_j의 최소 곱셈 횟수로 정의하고, dp 배열을 이용해 계산합니다. 초기에 dp[i][i]를 0으로 초기화하고, l을 2부터 n까지 반복문을 돌면서 대각선 방향으로 dp[i][j]를 계산합니다. dp[i][j]는 dp[i][k] + dp[k+1][j] + A_i~A_k와 A_{k+1}~A_j의 행렬곱의 곱셈횟수로 구할 수 있습니다. k는 i부터 j-1까지 반복합니다. 마지막으로 dp[1][n]을 반환하면 입력 행렬 곱셈의 최소 곱셈 횟수를 얻을 수 있습니다.
실행 결과
4500